Activity 2.4 - Experiment of Melde

Learning Aims:
  • Study the relation between the frequencies and standing waves in a vibrating string
  • Understanding concept of fundamental frequency and harmonics
Materials:
  • Function generator and mechanical vibrator
  • String
  • Pulley and weights to adjust the tension in the string
Suggestions for use:

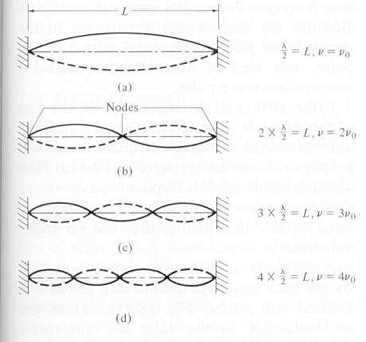
In this activity students perform ‘Melde’s experiment’ in which one end of a stretched string is attached to a vibrating support and the other end passes over a pulley to a hanging weight, which produces tension in a string. The stretched string is set in motion by the vibrating support, but if the frequency of vibration is not one of the natural frequencies (fundamental or harmonics) of the string the vibrational amplitude of the string is very small. However when the frequency of the vibrating support is the same as one of the natural frequencies the amplitude will be large and will clearly show patters (nodes and antinodes) of standing waves.

During the experiment the vibration frequency is changed and different patterns of resonant standing waves in a string are observed. The experiment is repeated for a different string tension.

Standing waves in a vibrating string, fundamental frequency and 1st. 2nd and 3rd harmonics.
Here, λ is a wavelength of standing wave, L is the length of the string, and υ is frequency of vibrations.

The harmonics are multiples of the fundamental frequency. So, a string of length L can vibrate with the fundamental frequency: f0 = v/2L and also with frequencies: f1 = 2 f0; f2 = 3 f0; f3 = 4f0 ; f4 =5f0 ; etc.

This experiment can be done as a demo for a class or in groups. Each group might use a different string tension. The students discover the similar standing wave patterns but for different frequencies. If there is time one might do this experiment with strings of different thickness.

If it is not possible to do this experiment in a classroom the different internet demo’s can be used, for example: http://youtu.be/_S7-PDF6Vzc or http://youtu.be/MT7EpS4OX3k .

Possible questions:
  • Draw different modes of vibrations for other sources (a string has both ends fixed but there are also musical instruments with one fixed end).
  • Are these different modes of vibrations also possible in a guitar?